project02 : Project-02 Fractal art: Spirals, trees and snowflakes

Goal

In you final lab you implemented recursive functions. It is time for you to start showing off your skills visually. In this project you will create some very cool fractal art, which is based on internal self-similarity. This project has a extra credit component where you can create a scene of your own choosing using the functions you implemented in the project.

Just like the previous project this assignment is out of 100 and have 10 points worth of extra credit. Note that there is no checkpoint for this assignment.

This project may be done individually or in pairs. If you are working with a pair indicate the name of both partners on top of each submission file.

Getting started

• Step 1: Log on & bring up a terminal window This is done following the steps you have performed in lab00.
• Step 2: Create a directory in your cs8 directory named project02.
• Step 3: Bring up idle and create two new files called recursiveDrawings.py in your ~/cs8/project02 directory.
• Step 4: For each of the programming exercises in this lab come up with a solution outline by discussing with your partner. Don’t be in a hurry to start coding unless you have a fairly clear idea of a solution strategy.

Draw a spiral…using recursion (10 pts)

In the file recursiveDrawings.py add a stub for the spiral function which has the following signature.

 spiral(initialLength, angle, multiplier)

The function takes as arguments

• an initialLength of the spiral’s first line segment,

• an angle specifying the angle (in degrees) formed by neighboring segments, and

• a multiplier indicating how each segment changes in size from the previous one.

For example, the following are example screenshots from the call spiral(100, 90, 0.9) and spiral(1, -45, 1.1), respectively:

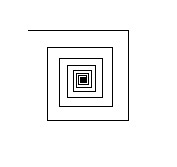
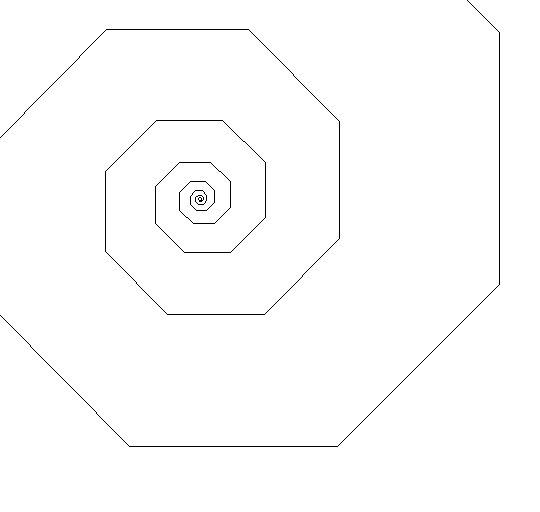
In the figure on the left the spiral is generated outside-in. This means it starts with initialLength 100 pixels. It turns right by 90 degrees to draw a successive segment whose length is 0.9 times that of the previous one. In the figure on the right, the spiral grows inside-out. It starts from the center with initialLength 1 pixel. Each iteration the line turns left by 45 degree and draw a segment whose length is 1.1 times longer.

Note the spiral function is computed inside-out, or outside-in, depending on the multiplier, therefore the base case varies. The spiral should stop drawing when it has reached a side length of less than 1 pixel (if multiplier<1) or greater than 200 pixels (if multiplier>1).

Implement the function and use it to draw an interesting spiral of your own.

Help! Stack Overflow! Do not be alarmed if you find you are getting stack overflow errors when you try to run the “growing spiral” example above. This error is caused by an infinite recursion. I.e. a recursion that never hits its base case. Not sure why? This is a perfect time to practice some of those debugging skills you learned above. :) Ask a tutor if you need help.

Grow a Tree (20 pts)

Next, you will write the tree function. It has the following signature:

 def tree(trunkLength, height)

The function takes as arguments:

• a trunkLength which is the length of the main trunk of the tree, and
• the height indicating the number of levels of branching of the tree. For example, the following is an example screenshot from the call to tree(200, 4):

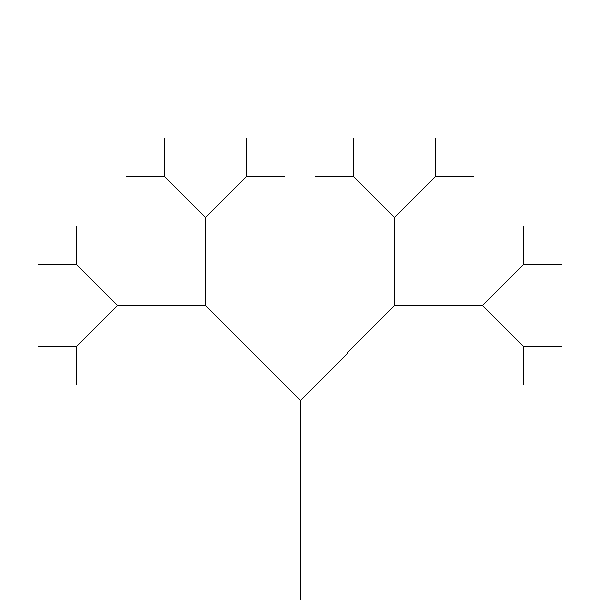
The tree “grows” from the ground from the current location of the turtle, with initial length of the first trunk 200 pixels. At the end of the first segment, the trunk forks into two directions. The forked trunk in each direction has a shorter length and continues to fork at the end, until the tree has forked 4 times.

Think about the base case and its recursive steps before implementing the function.

Your tree will be personalized by the aesthetic choices you make about

• the number of branches at each fork (anything greater than 1 is OK),

• the exact angle of branching,

• the reduction of trunkLength in sub-branches.

Your tree is planted on the ground and should grow upward.

Draw a few trees (20 pts)

Implement a function drawForest() with the following signature:

def forest( n, limits):

the function takes the following parameters

• the number of trees to draw: n
• a list of two tuples, limits: [(xmin, ymin), (xmax, ymax)].

Your function should draw n trees at random locations whose trunks originate within a bounding box whose lower left coordinate is (limits[0][0], limits[0][1]) and upper right coordinate is (limits[1][0], limits[1][1])

To draw the forest, call your tree() function in a for loop. You have to choose the trunkLength and height of your trees appropriately.

Note that your trees don’t have to look the same. Vary the trunkLength and height of your trees to create interesting variations.

This function should use for loops instead of recursion.

Extra credit: Create Snowflakes … in Santa Barbara! (8 pts extra credit)

Christmas is approaching and we need snowflakes in Santa Barbara. By completing this exercise you will not only add to the festivities but also prove that you are now very skilled at creating fractals using recursions.

In this exercise you will create the following snowflake structure (a.k.a. Koch Snowflake).

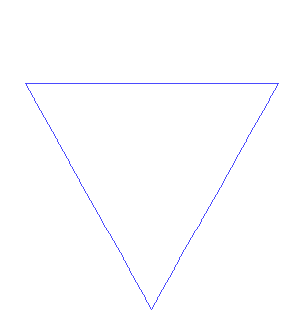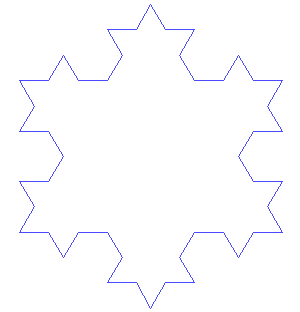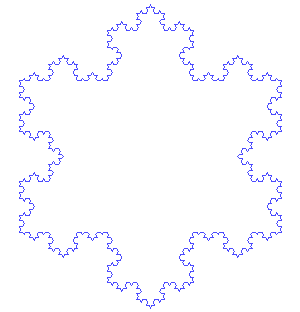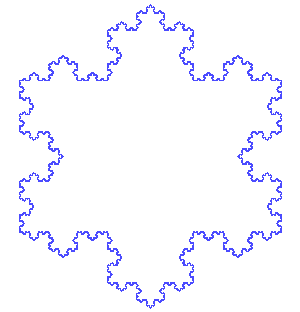
As the animation shows, the Koch snowflake begins with an equilateral triangle; at each stage, the middle third of each line segment is replaced by a pair of line segments that together with the replaced segment, form an equilateral triangle; then the replacement will be performed again on all the component line segments of the newly created shape, over and over.

We will draw the Koch Snowflake by first defining the snowflake function with the following signature:

snowflake(sideLength, levels)

which takes as arguments:

• a sideLength of the initial equilateral triangle, and

• the levels indicating the number of recursive levels performed to create the final snowflake.

Observe that the base case is simply an equilateral triangle with side length equal to sideLength. Each increment of level replaces the middle third of all of the snowflake’s sides with a “bump” that is, itself, a smaller equilateral triangle.

Hint: It might be useful to write a helper function with the following signature:

snowflakeSide(sideLength, levels)

The above functions should draw just one side of the underlying equilateral triangle – along with all of its squiggles or bumps, recursively!

All of the recursion will then be in snowflakeSide. So, first try creating snowflakeSide and make sure that it works and draws a single side of the snowflake curve at the appropriate level of recursion. Once snowflakeSide works, then your snowflake function will call snowflakeSide three times, with appropriate angles between them.

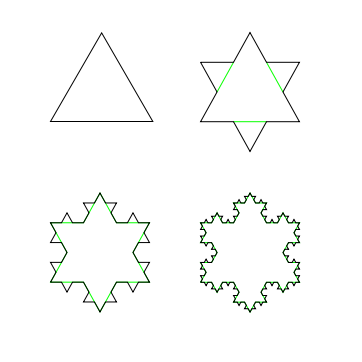
Again, in this strategy, all of the recursion occurs in snowflakeSide. Remember that if levels is zero, then snowflakeSide should produce a single line segment (this will be the base case of the recursion); otherwise, snowflakeSide needs to call itself four times; and, keep in mind that you’re only creating one of the three sides of the snowflake! Here are images of four steps (after three levels of recursions) of the overall Koch curve’s progression:

Test your implementation by calling snowflake(280, 4); you should get the following snowflake:

Drawing the snowflake is challenging. If you have completed this exercise consider it a major accomplishment!! Congratulations!!!

Draw a scene (Required) (20 pts + 2 pts of extra credit)

Define a function named scene that takes no parameters and makes a scenery by calling all the functions that you have implemented so far: spiral, forest, and/or snowflake.

Your scene should have more than one instance of each shape. You scene must have a forest of trees and some snow that may be a combination of calls to spiral and snowflake.

Call your scene function within a if __name__==__main__: clause and it should do all the work for you.

Extra credit (2 pts): Get creative with your scene by reusing the functions you have already implemented in interesting ways or writing enhanced versions of the functions. For example you may write a new tree function named decorativeTree that uses the spiral within the tree function to make it more decorative.

Take a snapshot of your final scene and save it as a jpg or png file. You will need to upload this on gauchospace along with you code

Submit on gauchospace

Go to gauchospace and navigate to the project02 assignment. Upload two files:

• a picture of your final scene
• your code recursiveDrawings.py

Make sure that your code runs without any errors. Code that produces errors will not be graded.

You do not need to submit your project on submit.cs

Here is a breakdown of the points for this project02

• Uploaded the two required files on gauchospace: 10 points
• Code executes without errors: 10 points
• All calls to functions are within the if __name__ ==__main__:clause: 10 pts
• Scene contains at least one spiral: 10 points
• Scene contains at least one tree: 20 points
• Scene contains at least three different trees: 20 points
• scene function makes appropriate calls to other functions to draw the final scene: 20 pts
• Extra credit:
  • Koch snowflake correctly implemented and used in the scene (8 pts)
  • Creative reuse of functions already implemented in design of scene and/or use of enhanced functions in scene: (2 pts)

Diba Mirza